主成分分析,PCA (Principal Component Analysis)
主成分分析(PCA)是一种降维方法,通常用于降低大型数据集的维度,通过将大型变量集转换为仍包含大型变量集中大部分信息的较小变量。减少数据集的变量数量自然会以牺牲准确性为代价,但降维的技巧是牺牲一点准确性来换取简单性。因为较小的数据集更容易探索和可视化,从而使机器学习算法分析数据点变得更加容易和更快,而无需处理无关变量。总而言之,PCA的思想很简单:减少数据集的变量数量,同时保留尽可能多的信息。

主成分是被构造为初始变量的线性组合或混合的新变量。这些组合以这样的方式完成:新变量(即主成分)是不相关的,并且初始变量内的大部分信息被挤压或压缩到第一成分中。因此,10 维数据的想法是给你 10 个主成分,但 PCA 尝试将最大可能的信息放入第一个成分中,然后将最大剩余信息放入第二个成分中,依此类推,直到得到如下屏幕图中所示的内容(横坐标是每个主成分排序,纵坐标是每个主成分的方差(信息)百分比)。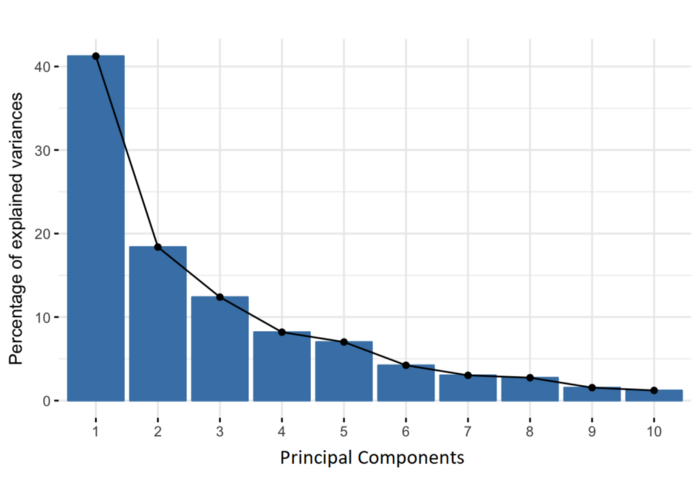
以这种方式组织主成分中的信息将允许您在不丢失太多信息的情况下降低维度,这是通过丢弃信息量低的成分并将剩余成分视为新变量来实现的。当然这也带来另一个问题,因为主成分分析后保留下来的每个主成分都是初始变量的线性组合的值,是一个单纯的标量,没有对应的实际意义。因此主成分的解释性非常差。
从几何上讲,主成分代表了解释最大方差的数据方向,即捕获数据大部分信息的线。这里方差与信息的关系是,一条线所携带的方差越大,沿该线的数据点的离散度就越大,而沿一条线的离散度越大,则该线所包含的信息越多。简而言之,只需将主成分视为新轴,它提供查看和评估数据的最佳角度,以便更好地看到观察结果之间的差异。
主成分分析过程感官介绍
由于数据中有多少个变量,就有多少个主成分,因此主成分的构造方式应使第一个主成分尽可能占数据集中最大的方差。例如,假设我们的数据集的散点图如下所示,我们可以就可以感官的猜测第一个主成分。大约是与紫色标记匹配的线,因为它穿过原点,并且我们的数据投影到这条线上的投影点(红点)最分散的线。或者从数学上讲,它是最大化方差(数据投影到这条线上后,从投影点(红点)到原点的平方距离的平均值)的线。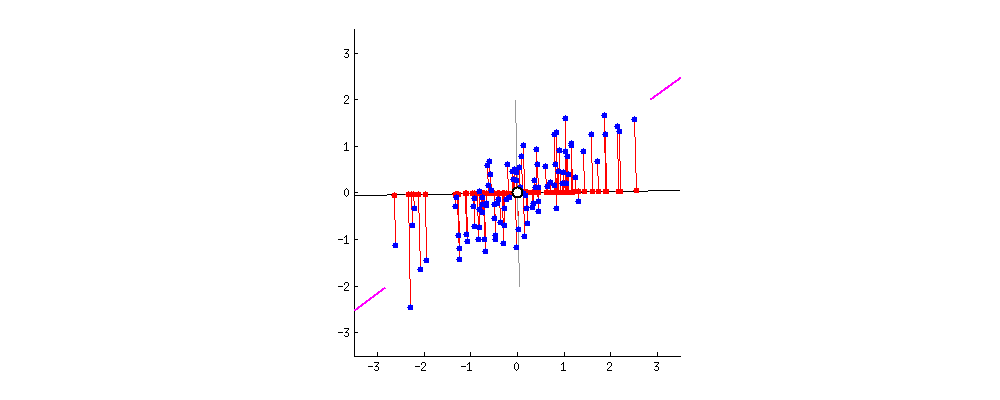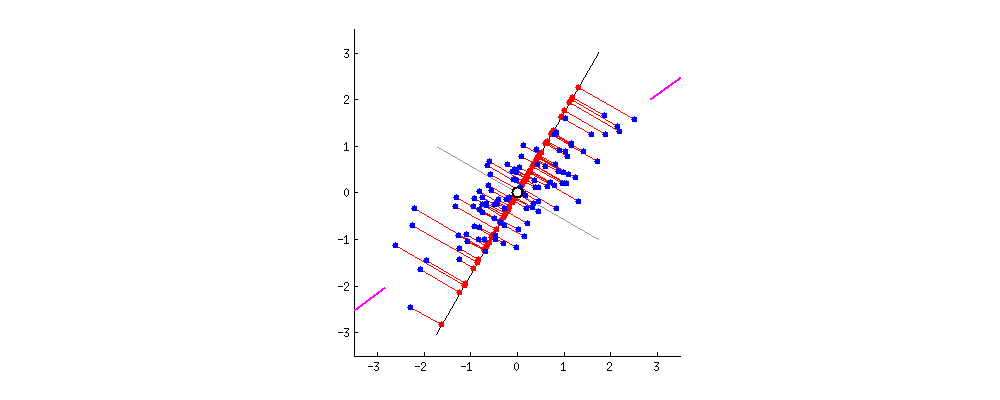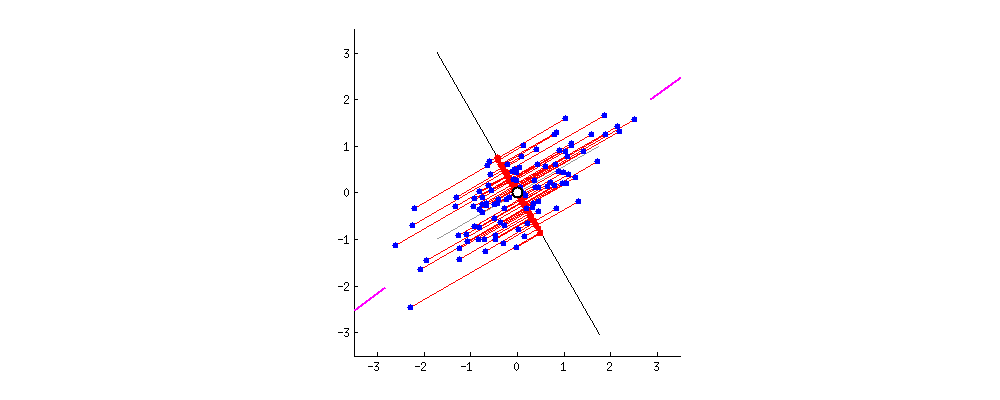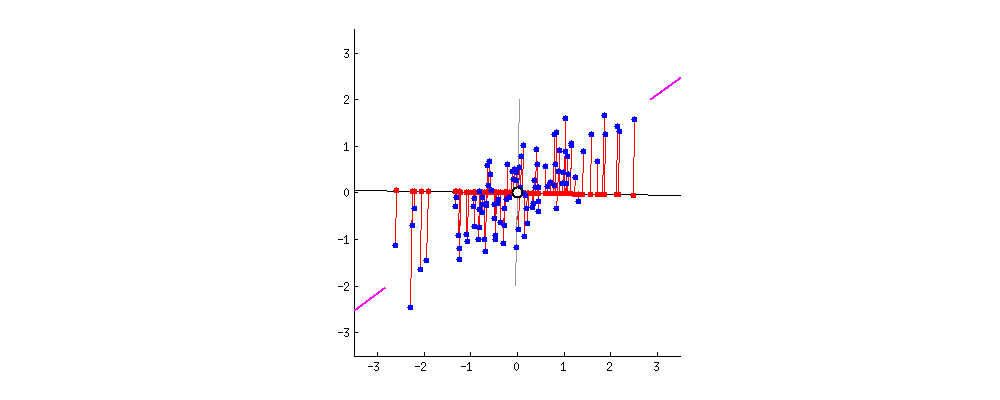
第一主成分我们是在平面展示的,现在我来想想一个3D数据集。在获取第一个主成分后,我们可以得到第一主成分的一个垂面。将我们的所有数据投影到垂面上,然后重复类似第一主成分获取的方式,就可以得到第二主成分。第二主成分和第一主成分不相关(即垂直)并且它解释了下一个最高方差。
针对高纬度的数据,我们以此类推重复此过程,一直持续到计算出总共p个主成分,等于原始变量数量。
理解信息量

上图中,如果我们单独看某一个维度的话,比如看x1这个维度
可以看到将点投影到x1这个维度上看的话,图1的数据离散性最高,图3较低,图2数据离散性是最低的。数据离散性越大,代表数据在所投影的维度上具有越高的区分度,这个区分度就是信息量。如果我们用方差来形容数据的离散性的话,就是数据方差越大,表示数据的区分度越高,也就是蕴含的信息量是越大的。
而我们进行降维的过程,就是用一个或几个较少的维度反应数据的信息量。从数据看,图1我们可以保留图x1维度,对应的图2可以保留x2维度来最大的反应数据的特征,但是相对图3,就是我们在PCA分析中要解决的问题,为了找到要给更好的维度,我们需要基于如下的方式,构建获取一个衡量体系(由原本的某2个或某几个特征组合而成)示例如下:
转换后,每个位点的特征表示方式,由原来的 (x1,x2) 转变为 (y1,y2)。
同时这时候我们把这个过程简化成一个数学运算,其实相当于是对每个特征点的 原始特征向量(每个维度的数据构成一个向量) * 一个矩阵(两个坐标体系的转移矩阵) 获得新的坐标轴体系(由特征向量确定的方向)上的特征值(在新坐标体系下的对应方向上的向量长度)。
主成分分析具体步骤
1. 标准化
PCA 对于初始变量的方差非常敏感,如果初始变量的范围之间存在较大差异,则范围较大的变量将主导范围较小的变量(例如,范围在 0 到 100 之间的变量将主导范围在 0 到 1 之间的变量),这会导致结果有偏差。所以需要在进行PCA分析前先要对数据进行标准化来消除初始变量范围差异带来的影响。标准化的过程就是将数据转换为可比较的尺度可以防止这个问题。
常见的步骤就是通过减去每个变量的每个值的平均值并除以标准差来完成。
$z=\frac{value-mean}{\sigma}$
标准化完成后,所有变量都将转换为相同的尺度,确保每个变量对分析的贡献相同。
2. 计算协方差矩阵
对所有的初始变量,计算协方差矩阵(协方差为正代表正相关,协方差为负代表负相关;数值越大相关性越强)。
3. 计算协方差矩阵的特征向量和特征值以识别主成分
特征向量和特征值是线性代数概念,我们需要根据协方差矩阵计算它们,以确定数据的主成分。
关于特征向量和特征值,您首先需要了解的是它们总是成对出现,因此每个特征向量都有一个特征值。此外,它们的数量等于数据的维数。例如,对于 3 维数据集,有 3 个变量,因此有 3 个特征向量和 3 个对应的特征值。
4. 创建特征向量
计算特征向量并按特征值降序对它们进行排序,使我们能够按重要性顺序找到主成分。在这一步中,我们要做的是选择是保留所有这些分量还是丢弃那些不太重要(低特征值)的分量,并与剩余的分量形成一个向量矩阵,我们称之为特征向量。
特征向量只是一个矩阵,其列是我们决定保留的分量的特征向量。这使其成为降维的第一步,因为如果我们选择仅保留n中的p 个特征向量(分量),则最终数据集将只有p 个维度。
5. 沿主成分轴重新构建数据
最后一步的目的就是使用协方差矩阵的特征向量形成的特征向量,将数据从原始轴重新定向到由主成分表示的轴(因此称为主成分分析) )。这可以通过将原始数据集的转置乘以特征向量的转置来完成。
注意事项
由于PCA算法的特征