线性回归模型简介

线性与非线性

线性：两个变量之间的关系是一次函数关系的——图象是直线，叫做线性。
注意：线性是指广义的线性，也就是数据与数据之间的关系。
非线性：两个变量之间的关系不是一次函数关系的——图象不是直线，叫做非线性。

线性回归是统计学中一种常用的预测分析方法，它通过最小化误差的平方和来研究变量之间的线性关系。线性回归模型可以是简单的一元线性回归，也可以是包含多个自变量的多元线性回归。

线性回归的基本概念

线性回归模型的基本形式可以表示为 $y = wx + e$，其中 $y$ 是因变量，$x$是自变量，$w$ 是回归系数，$e$ 是误差项，通常假设 $e$ 服从均值为 $0$ 的正态分布。在一元线性回归中，只包含一个自变量和一个因变量，而在多元线性回归中，包含两个或多个自变量。

线性回归的应用

线性回归广泛应用于各个领域，包括经济学、金融、医学和工程等。在经济学中，线性回归用于预测消费支出、投资支出等经济指标。在金融领域，它用于分析和计算投资的系统风险。在医学研究中，线性回归可以帮助分析吸烟对死亡率和发病率的影响。

线性回归的假设

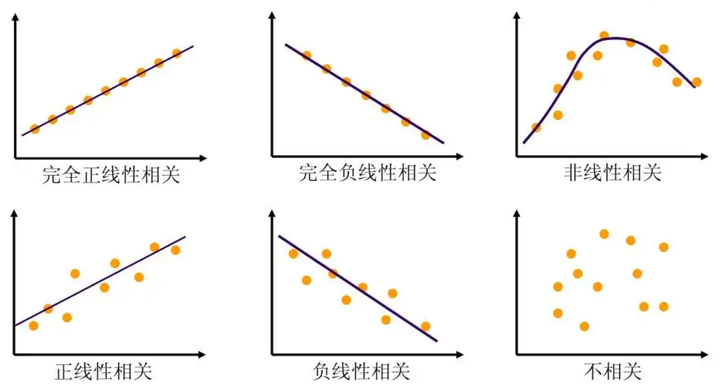
线性回归模型
从这四个数据集的分布可以看出，并不是所有的数据集都可以用一元线性回归来建模。现实世界中的问题往往更复杂，变量几乎不可能非常理想化地符合线性模型的要求。

为了有效地使用线性回归模型，需要满足几个基本假设：

自变量和因变量之间存在线性关系。
误差项应服从均值为零的正态分布。
自变量之间应相互独立，避免多重共线性问题。

线性回归的实现

线性回归模型可以通过最小二乘法来求解，得到回归系数和截距。在 Python 中，可以使用 sklearn.linear_model 中的 LinearRegression 类来实现线性回归模型。以下是一个简单的线性回归模型的实现示例：

import numpy as np
from sklearn.linear_model import LinearRegression

# 创建数据集
X = np.array([[1], [2], [3], [4], [5]])
y = np.array([1, 3, 2, 3, 5])

# 创建线性回归模型
model = LinearRegression()
model.fit(X, y)

# 打印模型系数和截距
print('系数:', model.coef_)
print('截距:', model.intercept_)

线性回归的优缺点

线性回归模型的优点包括模型简单、易于理解和实现，结果具有良好的可解释性。然而，它的缺点是对非线性数据建模能力有限，且当自变量之间存在相关性时，模型的预测性能会下降。

线性回归是一种强大且实用的工具，但在应用时需要仔细考虑其假设条件和适用范围。通过对数据进行适当的预处理和选择合适的模型，线性回归可以在许多领域提供有价值的洞察。