GBDT基本概念和简介
GBDT (Gradient Boosting Decision Tree) 是另一种基于 Boosting 思想的集成算法,除此之外 GBDT 还有很多其他的叫法,例如:GBM (Gradient Boosting Machine),GBRT (Gradient Boosting Regression Tree),MART (Multiple Additive Regression Tree) 等等。GBDT 算法由 3 个主要概念构成:Gradient Boosting (GB),Regression Decision Tree (DT 或 RT) 和 Shrinkage。
梯度提升决策树(GBDT)是一种特殊的提升算法,它使用决策树作为基学习器,并通过梯度下降方法优化损失函数。
从 GBDT 的众多别名中可以看出,GBDT 中使用的决策树并非我们最常用的分类树,而是回归树。分类树主要用于处理响应变量为因子型的数据,例如天气 (可以为晴,阴或下雨等)。回归树主要用于处理响应变量为数值型的数据,例如商品的价格。当然回归树也可以用于二分类问题,对于回归树预测出的数值结果,通过设置一个阈值即可以将数值型的预测结果映射到二分类问题标签上,即 $Y={-1,1}$。
对于 Gradient Boosting 而言,首先,Boosting 并不是 Adaboost 中 Boost 的概念,也不是 Random Forest 中的重抽样。在 Adaboost 中,Boost 是指在生成每个新的基学习器时,根据上一轮基学习器分类对错对训练集设置不同的权重,使得在上一轮中分类错误的样本在生成新的基学习器时更被重视。GBDT 中在应用 Boost 概念时,每一轮所使用的数据集没有经过重抽样,也没有更新样本的权重,而是每一轮选择了不用的回归目标,即上一轮计算得到的残差 (Residual)。其次,Gradient 是指在新一轮中在残差减少的梯度 (Gradient) 上建立新的基学习器。
所以在GBTD中,我们的目标其实已经发生了变化,实际上我们的建模目标是降低特定损失函数计算得到的残差(但是显而易见的残差越低,模型准确性越高)。
概念说明
残差:残差是实际值与预测值的差。针对预测问题,我们有预测函数$F(x)$,则第 $t$ 轮的预测值为 $F_t(x)$,第 $t$ 轮的残差为 $r_{t,i} = y_i - F_t(x_i)$。
GBDT的基本流程:
1. 初始化模型,通常是一个常数值
2. 计算当前模型的残差(实际值与预测值的差)
3. 训练一个新的决策树来拟合这些残差
4. 将新树添加到现有模型中
5. 重复步骤2-4直到满足停止条件
示例
下面我们通过一个年龄预测的 示例 简单介绍 GBDT 的工作流程。
假设存在 4 个人 (P = {p_1, p_2, p_3, p_4}),他们的年龄分别为 (14, 16, 24, 26)。其中 (p_1, p_2) 分别是高一和高三学生,(p_3, p_4) 分别是应届毕业生和工作两年的员工。利用原始的决策树模型进行训练可以得到如下图所示的结果: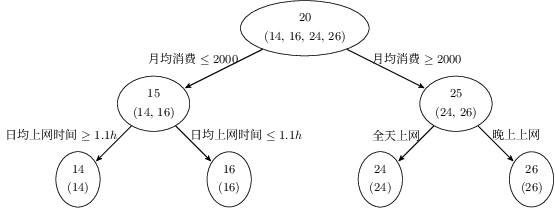
利用 GBDT 训练模型,由于数据量少,在此我们限定每个基学习器中的叶子节点最多为 2 个,即树的深度最大为 1 层。训练得到的结果如下图所示:
在训练第一棵树过程中,利用年龄作为预测值,根据计算可得由于 (p_1, p_2) 年龄相近,(p_3, p_4) 年龄相近被划分为两组。通过计算两组中真实年龄和预测的年龄的差值,可以得到第一棵树的残差 (R = {-1, 1, -1, 1})。因此在训练第二棵树的过程中,利用第一棵树的残差作为标签值,最终所有人的年龄均正确被预测,即最终的残差均为 (0)。
则对于训练集中的 4 个人,利用训练得到的 GBDT 模型进行预测,结果如下:
- (p_1) :14 岁高一学生。购物较少,经常问学长问题,预测年龄 (Age = 15 - 1 = 14)。
- (p_2) :16 岁高三学生。购物较少,经常回答学弟问题,预测年龄 (Age = 15 + 1 = 16)。
- (p_3) :24 岁应届毕业生。购物较多,经常问别人问题,预测年龄 (Age = 25 - 1 = 24)。
- (p_4) :26 岁 2 年工作经验员工。购物较多,经常回答别人问题,预测年龄 (Age = 25 + 1 = 26)。
整个 GBDT 算法流程如下所示:
GBDT 中也应用到了 Shrinkage 的思想,其基本思想可以理解为每一轮利用残差学习得到的回归树仅学习到了一部分知识,因此我们无法完全信任一棵树的结果。Shrinkage 思想认为在新的一轮学习中,不能利用全部残差训练模型,而是仅利用其中一部分,即:
$$ r_m = y - s F_m \left(x\right), 0 \leq s \leq 1 $$
注意,这里的 Shrinkage 和学习算法中 Gradient 的步长是两个不一样的概念。Shrinkage 设置小一些可以避免发生过拟合现象;而 Gradient 中的步长如果设置太小则会陷入局部最优,如果设置过大又容易结果不收敛。